教育・研究の内容
体とガロア理論
 2次方程式の解の公式を皆さんはご存知でしょう。3次・4次方程式の解も、同様にべき根で表すことができます。では5次方程式は?これは何世紀もの間、未解決問題でしたが、19世紀初頭に数学者ガロアが解の公式は存在しないことを示しました。画期的だったのは、「方程式がどう解けるか」が「解のもつ対称性による」という発見です。この対称性は、ガロア群と呼ばれています。授業では、方程式とガロア群の密接な対応について学びます。
2次方程式の解の公式を皆さんはご存知でしょう。3次・4次方程式の解も、同様にべき根で表すことができます。では5次方程式は?これは何世紀もの間、未解決問題でしたが、19世紀初頭に数学者ガロアが解の公式は存在しないことを示しました。画期的だったのは、「方程式がどう解けるか」が「解のもつ対称性による」という発見です。この対称性は、ガロア群と呼ばれています。授業では、方程式とガロア群の密接な対応について学びます。
関連科目:代数学I、代数学II、代数学III
ホモロジー論
 幾何学は「三角形の合同」や「円周角」など、直線や円で作られる図形の性質を調べる学問と一般に考えられていますが、「位相幾何学」という幾何学の分野では、球面やドーナツ面などの2次元の図形を含む、より高次元の図形(空間)を研究します。「ホモロジー」とは、位相幾何学における数学的な道具で、空間に対してアーベル群と呼ばれる足し算が定義された集合を対応させます。これによって目に見えない高次元の図形の性質を調べる方法を学びます。
幾何学は「三角形の合同」や「円周角」など、直線や円で作られる図形の性質を調べる学問と一般に考えられていますが、「位相幾何学」という幾何学の分野では、球面やドーナツ面などの2次元の図形を含む、より高次元の図形(空間)を研究します。「ホモロジー」とは、位相幾何学における数学的な道具で、空間に対してアーベル群と呼ばれる足し算が定義された集合を対応させます。これによって目に見えない高次元の図形の性質を調べる方法を学びます。
関連科目:幾何学I、幾何学II、幾何学III、幾何学IV
微分方程式論
 自然現象や社会現象における変化や変動の基本的なメカニズムは、微分方程式を用いて表されます。その微分方程式を解くことで変化の全体像を把握することができます。例えば、遠い惑星に宇宙探査機を飛ばせるのも、背景にある微分方程式の解析を通して、起こり得る事態を精密に予測できるからです。微分方程式は、工学・生物学・経済学・医学など幅広い分野で応用され、重要性が高まっています。授業では、微分方程式の解法を中心に学習します。
自然現象や社会現象における変化や変動の基本的なメカニズムは、微分方程式を用いて表されます。その微分方程式を解くことで変化の全体像を把握することができます。例えば、遠い惑星に宇宙探査機を飛ばせるのも、背景にある微分方程式の解析を通して、起こり得る事態を精密に予測できるからです。微分方程式は、工学・生物学・経済学・医学など幅広い分野で応用され、重要性が高まっています。授業では、微分方程式の解法を中心に学習します。
関連科目:解析学I、解析学II、解析学III、数値解析学、現代積分論、複素関数論、関数解析学、関数方程式論I、関数方程式論II
確率統計
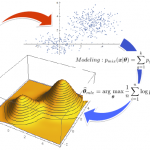 統計学は、観測されたデータから有用な情報を抽出することを目指しています。右図の散布図(上)には、二つの塊(クラスター)が見えます。これは、二つの異なる種類のデータが混在しているからでしょうか。それとも、一種類のデータが偶然二つの塊に見えるのでしょうか?このような判定を合理的に行うために、確率分布の概念を基礎にした統計的推測の理論を学びます。
統計学は、観測されたデータから有用な情報を抽出することを目指しています。右図の散布図(上)には、二つの塊(クラスター)が見えます。これは、二つの異なる種類のデータが混在しているからでしょうか。それとも、一種類のデータが偶然二つの塊に見えるのでしょうか?このような判定を合理的に行うために、確率分布の概念を基礎にした統計的推測の理論を学びます。
関連科目:確率統計I、確率統計II、数理統計学I、数理統計学II、応用統計学
符号理論
 現在、広く普及している右図のような2次元コードは、1次元コードとして先に普及したバーコードよりも遙かに多くの情報をより少ない面積で記録することができます。また、バーコードでは誤り検出しかできないのに対して、2次元コードは、1980年に音楽CDのために標準化されたリード・ソロモン符号を用いた誤り訂正機能を持っています。そのような誤り訂正符号を構成する代数的な理論や、誤り訂正の仕組みなどについて学びます。
現在、広く普及している右図のような2次元コードは、1次元コードとして先に普及したバーコードよりも遙かに多くの情報をより少ない面積で記録することができます。また、バーコードでは誤り検出しかできないのに対して、2次元コードは、1980年に音楽CDのために標準化されたリード・ソロモン符号を用いた誤り訂正機能を持っています。そのような誤り訂正符号を構成する代数的な理論や、誤り訂正の仕組みなどについて学びます。
関連科目:線形代数I、線形代数II、代数学I、代数学II、代数学III、情報理論、符号理論
複素解析
2次方程式の虚数解として導出された複素数ですが、ベクトル的な側面とド・モアブルの定理に見られるような波の側面を併せ持ちます。この複素数を用いた解析を学ぶことにより、実数の範囲で学んだ関数の解析的性質が、複素数の範囲における解析的性質の実数の世界に顔を覗かせている一面であることが理解できます。また、等角写像を用いることにより、航空機を飛ばせたりするなど、複素解析は流体力学や電磁気学などに応用されています。授業では、計算を中心とする領域を学んだのち、幾何学的あるいは代数的な理論を含めた領域を学習します。
関連科目:解析学I、解析学III、解析学IV、関数方程式論I、関数方程式論II、代数学I、代数学II、幾何学I、幾何学III、幾何学IV
確率論・数理ファイナンス
確率論は自然や社会経済に見られるランダムな現象を記述・解析するために使われます。ある現象が起こる頻度や、ランダム性が系の性質をどのように決定するかを、確率微分方程式や伊藤の公式に代表される確率解析の手法や解析学などの手法を使って調べます。特に、数理ファイナンスはランダムな動きをする株価や為替とそれらと関連付けられた金融派生商品との関係を確率論の手法を使って調べる学問です。授業では確率論の基礎、ランダム性を数学的に記述するために必要な測度論などを学びます。
関連科目:数理ファイナンスI、数理ファイナンスII

